Archive for the ‘MOŽEŠ DA SVRATIŠ I NA MATIŠ’ Category
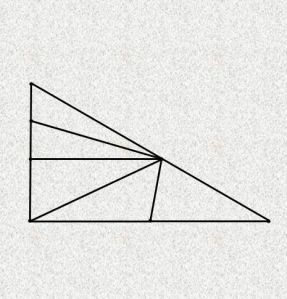
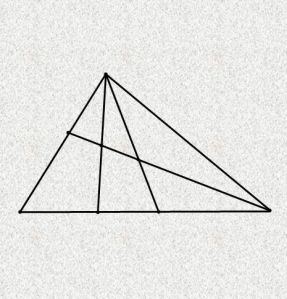
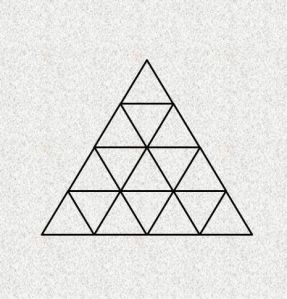
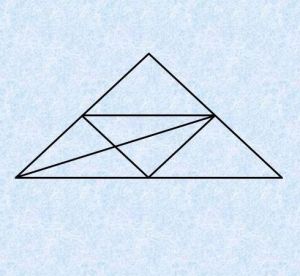
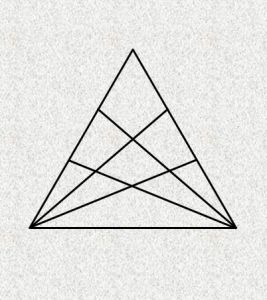
PRONAĐI TROUGLOVE
Posted on: 12. februara 2017.
Koliko trouglova ima na svakoj slici?
- Slika 1
- Slika 2
- Slika 3
- Slika 4
- Slika 5
- Slika 6
- Slika 7
- Slika 8
- Slika 9
- Slika 10
- Slika 11
- Slika 12
- Slika 13
- Slika 14
–
IV MATEMATIKA – PRELISTAVANJE
Posted on: 22. jula 2016.
Naučili smo iz matematike u IV razredu:
…
SKUP PRIRODNIH BROJEVA
Dekadne jedinice zapisane kao stepen broja deset
Čitanje i pisanje višecifrenih brojeva
Čitanje, pisanje, upoređivanje višecifrenih brojeva – vežbanje:
SABIRANJE I ODUZIMANJE U SKUPU PRIRODNIH BROJEVA
Sabiranje višecifrenih brojeva (1)
Sabiranje višecifrenih brojeva (2)
Sabiranje višecifrenih brojeva – vežbanje: 1, 2, 3
Veza sabiranja i oduzimanja
Zavisnost razlike od promene umanjenika
Zavisnost razlike od promene umanjioca
Oduzimanje višecifrenih brojeva (1)
Oduzimanje višecifrenih brojeva (2)
Oduzimanje višecifrenih brojeva (3)
Oduzimanje višecifrenih brojeva (4)
Oduzimanje višecifrenih brojeva – vežbanje: 1, 2, 3
Izračunavanje nepoznatog sabirka
Izračunavanje nepoznatog umanjenika
Izračunavanje nepoznatog umanjioca
Jednačine sa sabiranjem oduzimanjem
Jednačine: 1
Nejednačine sa sabiranjem i oduzimanjem
MNOŽENJE I DELJENJE U SKUPU PRIRODNIH BROJEVA
Zavisnost proizvoda od promene činilaca
Uloga nule i jedinice u množenju i deljenju
Množenje prirodnog broja dekadnom jedinicom
Množenje jednocifrenim brojem (1)
Množenje jednocifrenim brojem (2)
Množenje jednocifrenim brojem – vežbanje: 1, 2, 3
Množenje dvocifrenim brojem (1)
Množenje dvocifrenim brojem (2)
Množenje višecifrenim brojem (1)
Množenje višecifrenim brojem (2)
Veza množenja i deljenja
Deljenje zbira brojem
Deljenje razlike brojem
Zavisnost količnika od promene deljenika
Zavisnost količnika od promene delioca
Deljenje dekadnom jedinicom
Deljenje dekadnom (višestrukom dekadnom) jedinicom – vežbanje:
A, B, V
Deljenje višecifrenog broja jednocifrenim brojem (1)
Deljenje višecifrenog broja jednocifrenim brojem (2)
Deljenje višecifrenog broja jednocifrenim brojem (3)
Deljenje višecifrenog broja jednocifrenim brojem – vežbanje: 1, 2, 3, 4, 5
Deljenje višecifrenog broja dvocifrenim brojem
Deljenje višecifrenog broja višecifrenim brojem (1)
Deljenje višecifrenog broja višecifrenim brojem (2)
Deljenje višecifrenog broja višecifrenim brojem (3)
Izračunavanje nepoznatog činioca
Izračunavanje nepoznatog deljenika
Izračunavanje nepoznatog delioca
Jednačine sa množenjem i deljenjem
Nejednačine sa množenjem i deljenjem
MERENJE I MERE
Merenje zapremine
POVRŠINA
Površina figura
Jedinice mere za površinu
Površina pravougaonika
Površina kvadrata
Rogljasta i obla tela
Kvadar
Površina kvadra
Kocka
Površina kocke
RAZLOMCI
Razlomci
Pisanje i čitanje razlomaka
Upoređivanje razlomaka
III MATEMATIKA – PRELISTAVNJE
Posted on: 22. jula 2016.
Naučili smo iz matematike u III razredu:
…
BROJEVI PRVE HILJADE
Brojevi prve hiljade – vežbanje: A, B, V, G, D
Brojevi prve hiljade – vežbanje: 1, 2, 3, 4, 5, 6, 7, 8, 9
Pisanje brojeva rimskim ciframa
Rimski brojevi – vežbanje (ukrštenice): A, B, V
Rimski brojevi – vežbanje:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18
……………………………………….
SABIRANJE I ODUZIMANJE DO 1000
Sabiranje stotina – usmeno: A
Sabiranje trocifrenog i jednocifrenog broja – usmeno: A, B, V, G, D
Sabiranje trocifrenog i jednocifrenog broja – vežbanje: 1, 2, 3, 4, 5
…
Oduzimanje stotina – usmeno: A
Oduzimanje jednocifrenog od trocifrenog broja – usmeno: A, B, V, G
…
Sabiranje trocifrenog broja i desetica – usmeno: A, B, V, G, D
Sabiranje trocifrenog broja i desetica – vežbanje: 1, 2, 3, 4, 5, 6, 7
Sabiranje trocifrenog i dvocifrenog broja – usmeno: A, B, V
Sabiranje trocifrenog (dvocifrenog) i dvocifrenog broja – vežbanje:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
…
Oduzimanje desetica od trocifrenog broja – usmeno: A, B, V, G, D, Đ
Oduzimanje dvocifrenog od trocifrenog broja – usmeno: A, B, V
…
Sabiranje trocifrenih brojeva
Sabiranje trocifrenih brojeva – vežbanje: 1, 2, 3, 4, 5, 6, 7, 8, 9
Oduzimanje trocifrenih brojeva
Oduzimanje trocifrenih brojeva – vežbanje: 1, 2, 3
……………………………………….
MNOŽENJE I DELJENJE DO 1000
Zavisnost proizvoda od činilaca
Množenje brojem 10 i 100
Množenje jednocifrenog broja i desetica – vežbanje: A, B
Množenje jednocifrenog i dvocifrenog broja – vežbanje: 1, 2, 3
Množenje trocifrenog i jednocifrenog broja: A, B, V, G, D
…
Zavisnost količnika od deljenika
Zavisnost količnika od delioca
Deljenje brojem 10 i 100
Deljenje sa ostatkom – vežbanje: 1
Deljenje trocifrenog broja jednocifrenim brojem: A, B, V, G
Deljenje trocifrenog broja jednocifrenim brojem – vežbanje: 1, 2, 3, 4
……………………………………….
JEDNAČINE I NEJEDNAČINE
Izračunavanje nepoznatog sabirka
Nepoznati sabiak – vežbanje: 1, 2
Izračunavanje nepoznatog umanjenika
Izračunavanje nepoznatog umanjioca
Izračunavanje nepoznatog činioca
Izračunavanje nepoznatog deljenika
Izračunavanje nepoznatog delioca
Nejednačine sa sabiranjem
Nejednačine sa oduzimanjem
……………………………………….
MERENJE I MERE
Merenje dužine – vežbanje: 1
……………………………………….
GEOMETRIJA
Crtanje kružnice i kruga
Crtanje pravougaonika i kvadrata
Crtanje trougla
Geometrija – vežbanje: 1, 2, 3, 4, 5
……………………………………….
RAZLOMCI
Razlomci: polovina (1/2), četvrtina (1/4), osmina (1/8)
Razlomci: trećina (1/3), šestina (1/6)
Razlomci: petina (1/5), desetina (1/10)
Razlomci: sedmina (1/7), devetina (1/9)
II MATEMATIKA – PRELISTAVANJE
Posted on: 23. juna 2016.
PRIRODNI BROJEVI DO 100
Brojevi do 100 – vežbanje: 1, 2
Sabiranje jednocifrenih i dvocifrenih brojeva – usmeno: A
Sabiranje jednocifrenih i dvocifrenih brojeva – usmeno (vežbanje): 1, 2, 3, 4
Sabiranje dvocifrenih brojeva – usmeno: A, B, V
Sabiranje dvocifrenih brojeva – usmeno (vežbanje):
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Pismeno sabiranje dvocifrenih brojeva: A, B, V
…
Oduzimanje jednocifrenih od dvocifrenih brojeva – usmeno: A
Oduzimanje jednocifrenih od dvocifrenih brojeva – usmeno (vežbanje): 1, 2, 3
Oduzimanje dvocifrenih brojeva – usmeno: A, B, V
Oduzimanje dvocifrenih brojeva – usmeno (vežbanje): 1, 2, 3, 4, 5, 6, 7, 8, 9
Pismeno oduzimanje dvocifrenih brojeva: A, B, V
Sabiranje i oduzimanje (do 100): A, B, V, G, D, Đ, E
…
Sabiranje zbira brojem / Sabiranje razlike brojem
Oduzimanje zbira od broja / Oduzimanje razlike od broja
…
Izračunavanje nepoznatog sabirka
Izračunavanje nepoznatog sabirka – vežbanje: 1, 2
Izračunavanje nepoznatog umanjenika
Izračunavanje nepoznatog umanjioca
Izračunavanje nepoznatog umanjenika/umanjioca – vežbanje: 1, 2
Izračunavanje nepoznatog broja (sabirak/umanjenik/umanjilac): A, B
……………
Množenje broja 2 i brojem 2
Množenje broja 4 i brojem 4
Množenje broja 10 i brojem 10
Množenje broja 5 i brojem 5
Množenje brojevima 5, 10 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 2, 4, 10, 5 – vežbanje: 1, 2, 3, 4, 5
Množenje broja 3 i brojem 3
Množenje broja 6 i brojem 6
Množenje brojevima 3, 6 – vežbanje: 1, 2, 3, 4, 5
Množenje broja 7 i brojem 7
Množenje broja 8 i brojem 8
Množenje brojevima 6, 7, 8 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 7, 8 – vežbanje: 1, 2, 3, 4, 5
Množenje broja 9 i brojem 9
Množenje brojevima 5, 6, 7, 8, 9 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 7, 8, 9 – vežbanje: 1, 2, 3, 4, 5
Jedan i nula kao činioci
Množenje brojevima 0, 1, 2, 3, 4 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 1, 2, 3, 4, 5 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima od 0 do 10 – vežbanje: 1, 2, 3, 4, 5
Množenje zbira brojem / Množenje razlike brojem
Pismeno množenje dvocifrenog i jednocifrenog broja: A, B, V
Množenje dvocifrenog i jednocifrenog broja: 1, 2, 3, 4, 5, 6
Određivanje nepoznatog činioca
……………
Veza množenja i deljenja
Toliko puta manji broj (za toliko manji broj)
Redosled obavljanja računskih operacija
Deljenje dvocifrenog broja jednocifrenim: A, B, V (sa ostatkom)
Deljenje brojevima 1, 2, 3, 4 – vežbanje: A, B, V, G, D, Đ
Deljenje brojevima 1, 5, 10 – vežbanje: A, B
Deljenje brojevima od 1 do 10 – vežbanje: 1, 2, 3, 4, 5, 6, 7
Deljenje brojevima od 5 do 10 – vežbanje: 1, 2, 3
Deljenje brojevima od 6 do 10 – vežbanje: 1, 2, 3, 4, 5, 6
Deljenje – vežbanje: 1
Određivanje nepoznatog deljenika
Određivanje nepoznatog delioca
……………
MERENJE I MERE
……………
GEOMETRIJSKA TELA I FIGURE
Tela oblika lopte i valjka
Tela oblika kocke i kvadra
Paralelne prave / Normalne prave
MERENJE I MERE
Posted on: 15. januara 2016.
ГЕОМЕТРИЈА У РАВНИ
Posted on: 8. novembra 2015.
III разред – Геометрија (задаци за вежбање):
Геометрија (1) Геометрија (2) Геометрија (3)
Геометрија (4) Геометрија (5)
MATEMATIČKI IZRAZI
Posted on: 6. novembra 2015.
Klikni na sliku ili ovde.
ИЗРАЧУНАВАЊЕ НЕПОЗНАТОГ БРОЈА
Posted on: 16. oktobra 2015.
OSNOVNE RAČUNSKE OPERACIJE
Posted on: 11. septembra 2015.
PRVA STOTINA
Posted on: 5. septembra 2015.
BROJEVI DO 20
Posted on: 5. septembra 2015.
BROJEVI DO DESET
Posted on: 5. septembra 2015.
VUK, KOZA I KUPUS
Posted on: 25. aprila 2014.
Trebalo je da neki čovek čamcem preveze preko reke vuka, kozu i kupus. Ali, evo nevolje: čamac je bio tako mali da je u njega mogao da se smesti samo čovek, a s njim još ili vuk, ili koza, ili kupus. Ako na obali ostavi vuka i kozu, onda će vuk pojesti kozu. Ako ostavi kozu i kupus, onda će koza pojesti kupus. Međutim, u prisustvu čoveka „niko nikoga neće pojesti“.
Mada je situacija izgledala bezizlazna, ipak je čovek našao izlaz iz nje, tj. uspeo je da na tom čamcu sve preveze na drugu obalu reke. Kako je on to učinio?
Rešenje ovog zadatka, verovatno je mnogima već poznato. Za one koji ga ne znaju, biće sigurno jasnije ako ga vide u vidu stripa.
- Vuk ne jede kupus, zbog čega prevoženje treba početi s kozom. Vuka i kupus možemo ostaviti na obali i bez čoveka.

- Pošto je prevezao kozu na drugu obalu, čovek se vraća.

- Sada stavlja u čamac kupus i prevozi ga na drugu obalu. Međutim, ne zaboravite da kupus i koza ne smeju ostati zajedno!

- Ovoga puta ostavlja samo kupus, a kozu vraća kod vuka.

- Opet može doći do “neprijatne” situacije – koza i vuk zajedno… Da do toga ne bi došlo, čovek ostavlja kozu, a vuka vozi na desnu obalu.

- Ostavlja vuka i kupus.

- Konačno, vraća se po usamljenu kozu i prevozi je na drugu obalu reke.

Svi prevezeni preko reke i svi na broju: i vuk i koza i kupus. Zadatak rešen!
Izvor: Matematički list iz davne 1969. godine
STEPEN BROJA DESET
Posted on: 27. marta 2014.
Klikni na sliku ili ovde.
DEKADNE JEDINICE
Posted on: 27. marta 2014.
BAŠ JE ČUDAN
Posted on: 18. marta 2014.
![]() Jedan radnik, koji se nije mogao snaći u svom poslu, ode kod lekara da traži pomoć. Požali mu se na svoju nevolju. Lekar ga pregleda, pa mu reče:
Jedan radnik, koji se nije mogao snaći u svom poslu, ode kod lekara da traži pomoć. Požali mu se na svoju nevolju. Lekar ga pregleda, pa mu reče:
„Kao što je lav car među životinjama, tako je i lek, koji ću Vam prepisati, car među lekovima. Vrlo je efikasan, ali i čudan“. Zatim sede za sto i napisa recept: Car je čudan.
Dajući taj recept radniku, lekar mu objasni u koju apoteku treba da ide da bi mu na osnovu tog recepta sastavili lek.
Radnik je tu apoteku lako pronašao. Apotekar, kome se obratio, pogleda recept i reče radniku:
„U svaki lek ulaze pojedini sastojci u potrebnoj količini. Zato uzmite olovku pa ispod svakog slova u Vašem receptu (Car je čudan), napišite cifre redom od 1 do 9 i nulu. Na primer, ovako:
 Sada odaberite BILO KOJA tri slova iz recepta, pa ih zamenite odgovarajućim ciframa.
Sada odaberite BILO KOJA tri slova iz recepta, pa ih zamenite odgovarajućim ciframa.
Svaki lek mora da se meša. Zato dobijenom trocifrenom broju obrnite redosled cifara, pa od većeg broja oduzmite manji.
Dobijenoj razlici ponovo obrnite redosled cifara, pa je saberite s novodobijenim brojem (tj. „obrnutom“ razlikom). Tako ste dobili dozu leka za jedan dan.
Pošto mesec ima 30 dana, pomnožite dobijeni broj sa 30. Eto, to Vam je lek i on će Vam jedini pomoći u životu!“
„Ja Vas ništa ne razumem“, odgovori radnik.
„Zamenite cifre u dobijenom broju odgovarajućim slovima, pa će Vam sve biti jasno“, završi apotekar.
***
Ne zaboravite da možete uzeti bilo koje tri cifre. Rezultat će vas iznenaditi!
NEOBIČNE JEDNAKOSTI
Posted on: 18. marta 2014.
- Postoji nekoliko parova celih brojeva koji imaju zanimljivu osobinu: ZBIR i PROIZVOD svakog takvog para brojeva razlikuju se jedino u redosledu cifara.

- Neki parovi dvocifrenih brojeva imaju sasvim drugu, zanimljivu osobinu: PROIZVOD takvih parova brojeva, neće se promeniti ako se u svakom od činilaca cifre uzmu obrnutim redom.

- Evo i tri para uzastopnih brojeva čiji se kvadrati pišu istim ciframa, ali samo drugim redosledom:

PRIRODNI BROJEVI
Posted on: 12. oktobra 2013.
RIMLJANI BEZ NULE
Posted on: 30. septembra 2013.
 Stari Rimljani su od Grka naučili da broje. Kako se u njihovo doba ubrzano razvijala trgovina, rasla je potreba i da se brojevi zapisuju na što jednostavniji način. Tadašnji način zapisivanja brojeva došao je iz Grčke, ali je potekao sa istoka, a Rimljani su ga znatno usavršili. Zato je sedam simbola u ovom brojnom sistemu I, V, X, L, C, D i M nazvano rimske cifre.
Stari Rimljani su od Grka naučili da broje. Kako se u njihovo doba ubrzano razvijala trgovina, rasla je potreba i da se brojevi zapisuju na što jednostavniji način. Tadašnji način zapisivanja brojeva došao je iz Grčke, ali je potekao sa istoka, a Rimljani su ga znatno usavršili. Zato je sedam simbola u ovom brojnom sistemu I, V, X, L, C, D i M nazvano rimske cifre.
Među rimskim ciframa nema nule, pošto nekada nije bilo poznato da je i nula broj. Da bi se rimske cifre u nekom tekstu razlikovale od velikih latiničnih slova, najčešće se pisala i crta iznad njih. Ovaj način pisanja koristili su kasnije i Vizantijci, ali se danas više tako ne piše.
ПИСМЕНО ОДУЗИМАЊЕ (ДO 1000)
Posted on: 12. maja 2013.
ПИСМЕНО САБИРАЊЕ (ДО 1000)
Posted on: 12. maja 2013.
TESTOVI 2009. – MATEMATIKA IV
Posted on: 30. marta 2013.
MATEMATIKA I SAOBRAĆAJ
Posted on: 12. marta 2013.
UPOREĐIVANJE I MERENJE POVRŠI
Posted on: 10. marta 2013.
TAKMIČENJA – III i IV razred
Posted on: 31. januara 2013.
***
2008. – Školsko takmičenje iz matematike – III razred
2009. – Školsko takmičenje iz matematike – III razred
2011. – Školsko takmičenje iz matematike – III razred
2012. – Školsko takmičenje iz matematike – III razred
2013. – Školsko takmičenje iz matematike – III razred
2014. – Školsko takmičenje iz matematike – III razred
2015. – Školsko takmičenje iz matematike – III razred
2016. – Školsko takmičenje iz matematike – III razred
2017. – Školsko takmičenje iz matematike – III razred
2018. – Školsko takmičenje iz matematike – III razred
***
2006. – Opštinsko takmičenje iz matematike – III razred
2007. – Opštinsko takmičenje iz matematike – III razred
2008. – Opštinsko takmičenje iz matematike – III razred
2009. – Opštinsko takmičenje iz matematike – III razred
2010. – Opštinsko takmičenje iz matematike – III razred
2011. – Opštinsko takmičenje iz matematike – III razred
2012. – Opštinsko takmičenje iz matematike – III razred
2013. – Opštinsko takmičenje iz matematike – III razred
2014. – Opštinsko takmičenje iz matematike – III razred
2015. – Opštinsko takmičenje iz matematike – III razred
2016. – Opštinsko takmičenje iz matematike – III razred
2017. – Opštinsko takmičenje iz matematike – III razred
2018. – Opštinsko takmičenje iz matematike – III razred
***
Školsko takmičenje – IV razred:
1987. / 1988. / 1989. / 1990. / 1991. / 1992. / 1993. /
1994. / 1995. / 1996. / 1997. / 1998. / 1999. / 2000. / 2001.
2002. – Školsko takmičenje iz matematike – IV razred
2003. – Školsko takmičenje iz matematike – IV razred
2004. – Školsko takmičenje iz matematike – IV razred
2005. – Školsko takmičenje iz matematike – IV razred
2006. – Školsko takmičenje iz matematike – IV razred
2008. – Školsko takmičenje iz matematike – IV razred
2009. – Školsko takmičenje iz matematike – IV razred
2011. – Školsko takmičenje iz matematike – IV razred
2012. – Školsko takmičenje iz matematike – IV razred
2013. – Školsko takmičenje iz matematike – IV razred
2014. – Školsko takmičenje iz matematike – IV razred
2015. – Školsko takmičenje iz matematike – IV razred
2016. – Školsko takmičenje iz matematike – IV razred
2017. – Školsko takmičenje iz matematike – IV razred
2018. – Školsko takmičenje iz matematike – IV razred
***
Opštinsko takmičenje – IV razred:
1987. / 1988. / 1989. / 1990. / 1991. / 1992. / 1993. /
1994. / 1995. / 1996. / 1997. / 1998. / 1999. / 2000.
2001. – Opštinsko takmičenje iz matematike – IV razred
2002. – Opštinsko takmičenje iz matematike – IV razred
2003. – Opštinsko takmičenje iz matematike – IV razred
2004. – Opštinsko takmičenje iz matematike – IV razred
2005. – Opštinsko takmičenje iz matematike – IV razred
2006. – Opštinsko takmičenje iz matematike – IV razred
2007. – Opštinsko takmičenje iz matematike – IV razred
2008. – Opštinsko takmičenje iz matematike – IV razred
2009. – Opštinsko takmičenje iz matematike – IV razred
2010. – Opštinsko takmičenje iz matematike – IV razred
2011. – Opštinsko takmičenje iz matematike – IV razred
2012. – Opštinsko takmičenje iz matematike – IV razred
2013. – Opštinsko takmičenje iz matematike – IV razred
2014. – Opštinsko takmičenje iz matematike – IV razred
2015. – Opštinsko takmičenje iz matematike – IV razred
2016. – Opštinsko takmičenje iz matematike – IV razred
2017. – Opštinsko takmičenje iz matematike – IV razred
2018. – Opštinsko takmičenje iz matematike – IV razred
***
2000. – Okružno takmičenje iz matematike – IV razred
2001. – Okružno takmičenje iz matematike – IV razred
2002. – Okružno takmičenje iz matematike – IV razred
2003. – Okružno takmičenje iz matematike – IV razred
2004. – Okružno takmičenje iz matematike – IV razred
2007. – Okružno takmičenje iz matematike – IV razred
2008. – Okružno takmičenje iz matematike – IV razred
2009. – Okružno takmičenje iz matematike – IV razred
2010. – Okružno takmičenje iz matematike – IV razred
2011. – Okružno takmičenje iz matematike – IV razred
2012. – Okružno takmičenje iz matematike – IV razred
2013. – Okružno takmičenje iz matematike – IV razred
2014. – Okružno takmičenje iz matematike – IV razred
2015. – Okružno takmičenje iz matematike – IV razred
2016. – Okružno takmičenje iz matematike – IV razred
2017. – Okružno takmičenje iz matematike – IV razred
2018. – Okružno takmičenje iz matematike – IV razred
***
2005. – Kengur bez granica, III i IV razred / Rešenja
2006. – Kengur bez granica, III i IV razred / Rešenja
2007. – Kengur bez granica, III i IV razred / Rešenja
2008. – Kengur bez granica, II razred / III i IV razred / Rešenja
2009. – Kengur bez granica, II razred / III i IV razred / Rešenja
2010. – Kengur bez granica, II razred / III i IV razred / Rešenja
2011. – Kengur bez granica, II razred / III i IV razred / Rešenja
2012. – Kengur bez granica, II razred / III i IV razred / Rešenja
2013. – Kengur bez granica, II razred / III i IV razred / Rešenja
2014. – Kengur bez granica, I razred / II razred / III i IV razred / Rešenja
2015. – Kengur bez granica, I razred / II razred / III i IV razred / Rešenja
2016. – Kengur bez granica, I razred / II razred / III i IV razred / Rešenja
ZADATAK O DECEMBRU
Posted on: 29. januara 2013.
„Ja, drugovi, izučavam jezike, daleko sam od svake matematike“, poče čovek u godinama na koga je došao red da postavi zadatak.
„Zato ne očekujte od mene matematički zadatak. Mogu samo da vam postavim pitanje iz oblasti koju poznajem. Dopuštate li da vam postavim jedan zadatak iz kalendara?“
„Izvolite!“
„Dvanaesti mesec zovemo ‘decembar’. A da li znate šta ustvari znači ‘decembar’? Ova reč dolazi od grčke reči ‘deka’ – deset, od nje dolaze i reči ‘dekalitar’ – deset litara, ‘dekada’ – deset dana i dr. Izlazi da mesec decembar znači ustvari ‘deseti’. Kako objašnjavate ovo neslaganje?“
REŠENJE:
Naš kalendar vodi svoje poreklo od kalendara starih Rimljana. Rimljani, pak (do Julija Cezara), nisu računali početak godine od prvog januara, nego od prvog marta. Prema tome, decembar je tada bio deseti mesec.
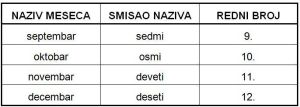
Kad je početak godine prenet na prvi januar, nisu bili izmenjeni nazivi meseca. Otud je i nastupilo to neslaganje između naziva i rednog broja, koje postoji sada za niz meseca.
Preuzeto iz knjige: „Zanimljiva matematika“ J. I. Pereljman
ARITMETIČKA PODVALA
Posted on: 29. januara 2013.
„Ja sam poslednji po redu, dvanaesti. Radi raznovrsnosti pokazaću vam jednu aritmetičku podvalu i zamoliću vas da otkrijete njenu tajnu. Neka ma ko od vas, recimo vi, druže predsedavajući, napiše na komadiću hartije proizvoljan trocifren broj, ali da ja ne vidim.
„Mogu li da budu i nule u tom broju?“
„Ne stavljam nikakva ograničenja. Koji god želite trocifren broj“.
„Napisao sam. Šta sad?“
„Dopišite mu taj isti broj. Sad ste dobili šestocifreni broj“.
„Da. Šestocifreni broj“.
„Predajte hartiju susedu koji sedi podalje od mene. A on neka podeli taj šestocifreni broj sa sedam“.
„Lako je reći: neka podeli! Možda nije deljiv.
„Ne uzbuđujte se, podeliće se i bez ostatka“.
„Ne znate broj, a znate da će se podeliti“.
„Najpre podelite, a posle ću da govorim“.
„Na vašu sreću podelio se“.
„Rezultat predajte svome susedu ne saopštavajući mi ga. Neka ga on podeli sa 11“.
„Mislite da će opet poći za rukom da se podeli?“
„Delite, ostatka nećete dobiti“.
„Predajte rezultat dalje. Podelite ga… pa, recimo, sa 13“.
„Niste dobro izabrali. Malo se brojeva mogu podeliti sa 13 bez ostatka… Gle, nije, podeli se do kraja. Uspelo vam je!“
„Dajte mi hartijicu s rezultatom; samo je savijte da ne vidim brojeve“.
Ne otvarajući listić hartije „podvaldžija“ ga predade predsedavajućem.
„Izvolite broj koji ste zamislili. Je li tačno?“
„Potpuno isti!“ sa zaprepašćenjem odvrati ovaj zagledavši se u listić hartije. „Taj sam baš i zamislio… sad, pošto je spisak govornika iscrpen, dopustite da zaključim naš skup. Srećom i kiša je prestala. Rešenja sviju zadataka objavićemo danas, posle užine. Cedulje s rešenjima možete da predajete meni“.
REŠENJE:
Pratimo šta je bilo urađeno sa zamišljenim brojem. Pre svega, njemu je dopisan još jedanput uzeti trocifreni broj. To znači isto što i dopisati tri nule i tako dobijenom broju dodati prvobitni trocifreni broj, npr.
872 872 = 872 000 + 872
Sad je jasno šta je u suštini bilo urađeno s brojem: on je uvećan 1000 puta, i osim toga, dodata mu je prvobitna vrednost; kraće rečeno, broj je pomnožen sa 1001.
Šta je zatim bilo urađeno s tim proizvodom? On je podeljen uzastopno sa 7, 11 i 13. On je, znači, ukupno deljen sa 7 x 11 x 13, tj. sa 1001.
Tako je zamišljeni broj prvo pomnožen sa 1001, a zatim podeljen sa 1001. Da li se treba čuditi što je kao rezultat dobijen taj isti broj?
Preuzeto iz knjige: „Zanimljiva matematika“ J. I. Pereljman
MNOŽENJE NA JAPANSKI NAČIN
Posted on: 20. januara 2013.
Pročitah negde da ovako množe mali Japanci. Da li oni, ili neko drugi, svejedno. Vrlo je zanimljivo.
– Vodoravnim linijama su predstavljene cifre prvog činioca.
– Uspravne linije su cifre drugog činioca.
– Tačke u kojima se ukrštaju vodoravne i uspravne linije su cifre proizvoda.
Tačke ukrštanja linija (dole desno) je cifra jedinica proizvoda koji ćemo dobiti (zaokružene zeleno). Crveno zaokružene su desetice, a plavo – stotine.
Na prvoj slici imamo: 21 x 22 = 462

Ja sam se malo poigrala, pa sam množila i veće brojeve. Kod njih treba samo prebaciti desetice i stotine (kad prelaze deset), ali mislim da to nije veliki problem jer su slike vrlo jasne.
Na drugoj slici, činioci su 17 i 13. Rezultat 221.
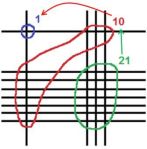
Kako ide sa još većim brojevima, ne znam, nisam dalje eksperimentisala.
A neverne Tome, ako baš ne veruju, mogu i da prebroje tačke u kojima se ukrštaju linije! 🙂
MALO DRUGAČIJE
Posted on: 18. decembra 2012.
Vredi pokušati… 🙂

Indijanski brojevi
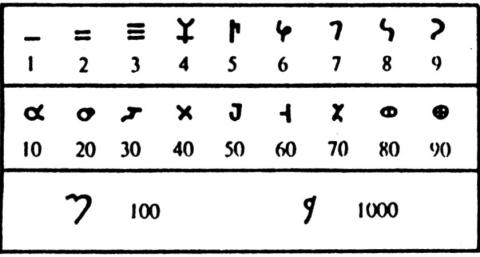
BABA CICA
Posted on: 3. novembra 2012.
Početkom trećeg razreda, iz matematike, deca uče rimske cifre tj. pisanje rimskih brojeva. Da li zato što ne liče na brojeve koje do tada koristimo, ili zato što deluju kao neke „tajne šifre“, uglavnom, deci se rimski brojevi posebno dopadaju.
Za pisanje rimskih brojeva treba zapamtiti sedam slova latinice.
Pisanje brojeva do 39 ide lako. Koriste se samo I, X i V, pa je važno da naučimo kako se pišu brojevi do deset i da zapamtimo pravilo, da se I i X ne pišu nikad više od tri puta. Pošto se ovi brojevi češće koriste (na satovima, kalendarima, za pisanje datuma i sl.), ne predstavljaju im poseban problem.
Za pisanje brojeva većih od 39, pojavljuju se i nove cifre. Da bi ih lakše zapamtili, ja u dogovoru sa decom, uvek primenim jedan trik. A trik se sastoji u sledećem: svako slovo koje koristimo, povežemo vizuelno sa nekom osobom tj. njegovim/njenim imenom.
Tako smo se, ove godine, dogovorili da je Lazar rimski broj 50 (L), Dimitrije – 500 (D). Slovo M nam nikad ne manjka, jer uvek imamo u odeljenju ili Miloša, Marka, Milicu… Međutim, zapelo je kod broja 100 tj. slova C. Nemamo nikog ko se zove na C, nemamo nikog ko se preziva na C… A broj 100 nam je posebno važan…
„Jedino ako može moja baba Cica“, kaže stidljivo Milica i svi prasnu u smeh. Naravno, predlog je odmah usvojen, a Milica je postala broj 1000, jer je u rodbinskoj vezi sa baba Cicom, pa da ih ne razdvajamo.
I, onda počinje prava zabava…
Kada neko piše broj na tabli, ostali spontano, horski, izgovaraju imena onih koje smo odredili za rimske cifre, pa to zvuči, otprilike, ovako:
broj 251 bi bio: baba Cica, baba Cica, Lazar, jedan tj. I (CCLI) ili
broj 740: Dimitrije, baba Cica, baba Cica, deset od Lazara (DCCXL)…
 Pošto Milica svoju babu ne zove nikad Cica, nego samo „baba“, ona je posebno izazivala smeh pišući brojeve. Na primer, broj 412 je bio „babu oduzmem od Dimitrija i dodam dvanaest“…
Pošto Milica svoju babu ne zove nikad Cica, nego samo „baba“, ona je posebno izazivala smeh pišući brojeve. Na primer, broj 412 je bio „babu oduzmem od Dimitrija i dodam dvanaest“…
Tako je izgledalo veselo učenje rimskih brojeva…
Posle petnaestak dana, setim se ja da proverim trajnost znanja o rimskim ciframa. Kažem: „Napišite broj 902…“ Samo što sam izgovorila to, jedan dečak ustade i viknu ostalima: „Znate valjda, Cica Milicina i dva!“ Moram priznati da mi do tog trenutka uopšte nije palo na pamet da je „Cica Milicina“ broj 900 (CM), pa sam bila pomalo zatečena… Ono što odraslima ponekad promakne, ne znači da će promaći i deci… I dobismo „šifru“ za broj 900 – Cica Milicina…
Posle ove školske godine, meni će lično, rimski broj 100 verovatno još dugo ostati asocijacija za baba Cicu, a nadam se i učenicima mog odeljenja… Setila sam se, čak, da ćemo sledeće godine imati i „Milicu Cicinu“… 🙂
TANGRAM
Posted on: 29. oktobra 2012.
Tangram ili „matematička zagonetka“, kako je još zovu, je zabavna slagalica koja vodi poreklo iz Kine i pretpostavlja se da je stara preko 3000 godina.
„Zagonetka“ je sastavljena od 7 delova koji su isečeni iz jednog kvadrata (paralelogram, kvadrat i 5 trouglova). Pravilo je da se delovi ne smeju preklapati, niti se bilo koji od njih sme izostaviti pri sastavljanju neke figure.
Od ovih delova može se sastaviti više od 1000 različitih figura.
Tangram se može igrati on-line, ali je dobro i malo koristiti papir, crtati trouglove, kvadrate, proračunavati i naravno – odmoriti oči od računara. 🙂

Neke od figura koje treba sastaviti:
 Rešenja su ovde…
Rešenja su ovde…
Ili možda ove…

O izboru figura koje možete sastavljati odlučite sami. Izbor je zaista veliki.
MATEMATIKA – IGRICE
Posted on: 29. oktobra 2012.
- Jednocifreni /dvocifreni /trocifreni brojevi: Fruit Shoot Place Value
- Sabiranje (do 20): Feed Fribbit Addition
- Množenje (do 100): Feed Fribbit Multiplication, Flying High,
- Sabiranje, oduzimanje, množenje, deljenje (do 100):
- Red računskih operacija (sastavi izraz): Order of Operations
- Oblici: Shape Inlay, Tangrams
- Nacrtaj…: Dupligon
- Merenje dužine (jedinice): Metric Length
- Merenje tečnosti (jedinice): Metric Volume
- Masa (Šta je teže?): Balance Scales
- Merenje vremena:Stop the Clock, Bang on time, Online-stopwatch
- Koliko ima kockica?: Cube Perspective
- Razlomci: Equivalent Fractions Shoot
ЦИФРЕ И БРОЈЕВИ
Posted on: 6. oktobra 2012.
 Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (1) / Вежбање (2) / Вежбање (3)
Вежбање (А) /Вежбање (Б) /Вежбање (В)
Вежбање (1) / Вежбање (2) / Вежбање (3)
Бројеви до 1000 – задаци за вежбање

RIMSKI BROJEVI
Posted on: 28. septembra 2012.
ODUZIMANJE DO 1000
Posted on: 13. septembra 2012.
ODUZIMANJE JEDNOCIFRENOG OD TROCIFRENOG BROJA
ODUZIMANJE DVOCIFRENOG OD TROCIFRENOG BROJA
ODUZIMANJE TROCIFRENIH BROJEVA
Oduzimanje jednocifrenog broja od višestrukih stotina/desetica: A, B
Oduzimanje jednocifrenog od trocifrenog broja (sa/bez prelaza):
Oduzimanje višestrukih desetica (sa prelazom): A, B
Oduzimanje višestruke desetice od trocifrenog broja: A, B
Oduzimanje dvocifrenog broja od višestruke stotine: A
Oduzimanje dvocifrenog od trocifrenog broja (bez prelaza): A
SABIRANJE DO 1000
Posted on: 13. septembra 2012.
SABIRANJE TROCIFRENOG I JEDNOCIFRENOG BROJA
SABIRANJE TROCIFRENOG I DVOCIFRENOG BROJA
SABIRANJE TROCIFRENIH BROJEVA
Sabiranje trocifrenog i jednocifrenog broja:
1, 2, 3, 4, 5
Sabiranje trocifrenog broja i višestruke desetice:
1, 2, 3, 4, 5, 6, 7
Sabiranje trocifrenog i dvocifrenog broja:
1, 2, 3, 4, 5, 6, 7
Sabiranje dvocifrenih brojeva:
1, 2, 3, 4
Sabiranje trocifrenih brojeva:
1, 2, 3, 4, 5, 6
ОДУЗИМАЊЕ ДО 100
Posted on: 2. septembra 2012.
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Одузимање (до 100) – вежбање: 1, 2, 3, 4, 5
САБИРАЊЕ ДО 100
Posted on: 2. septembra 2012.
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Вежбање (А) / Вежбање (Б) / Вежбање (В)
Сабирање до 100 – вежбање: 1, 2
DELJENJE
Posted on: 11. jula 2012.
MNOŽENJE
Posted on: 8. jula 2012.
Množenje (do 100)
Množenje brojevima 5, 10 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 2, 4, 10, 5 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 3, 6 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 6, 7, 8 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 7, 8 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 5, 6, 7, 8, 9 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 7, 8, 9 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 0, 1, 2, 3, 4 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima 1, 2, 3, 4, 5 – vežbanje: 1, 2, 3, 4, 5
Množenje brojevima od 0 do 10 – vežbanje: 1, 2, 3, 4, 5
Množenje (do 1000)
Množenje jednocifrenog i dvocifrenog broja A, B, C
Množenje (preko 1000)
Množenje dvocifrenih dvocifrenim brojevima: A, B, C
Množenje trocifrenih i jednocifrenih brojeva: A, B
Množenje višecifrenih i dvocifrenih brojeva: A, B
Množenje višecifrenih i dvocifrenih (trocifrenih) brojeva: A
Množenje višecifrenih i trocifrenih brojeva: A, B, C, D, E



























































































































































You must be logged in to post a comment.